Energieerhaltung bei schiefen Ebenen mit Reibung - Klausur- und Abiturvorbereitung Oberstufe

1. In Kapitel 4 haben wir gelernt, warum in einem abgeschlossenen System, die Energie erhalten bleibt. In dieser Lektion werden wir die Energieerhaltung auf Aufgaben bezüglich der schiefen Ebene anwenden. Dabei werden wir die Gleitreibung berücksichtigen. Folgende Begriffe und Größen musst du kennen:
2. Wir haben in Kapitel 3 die Gleitreibungskraft auf einer schiefen Ebene hergeleitet . Wenn ein Objekt auf einer schiefen Ebene ruht, d. h. sich nicht bewegt, dann verwenden wir die Normalkomponente ($F_N$) der Gewichtskraft zur Bestimmung der Größe Haftreibung. Die Richtung der Haftreibung ist antiparallel zur Parallelkomponente ($F_P$) der Gewichtskraft (s. Abbildung 1).
  
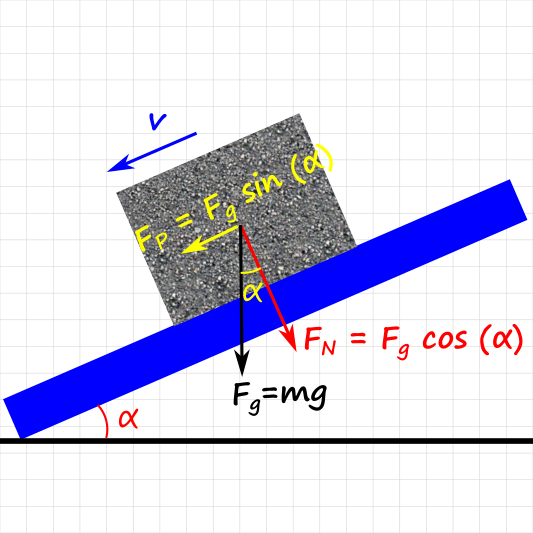
  Abbildung 1: Die relevanten Kräfte auf einer schiefen Ebene. $F_g$ ist die Gewichtskraft des Objekts, $F_P$ ist die Komponente der Gewichtskraft, die parallel zur Oberfläche der schiefen Ebene zeigt, $F_N$ ist die Normalkomponente der Gewichtskraft, die senkrecht zur Oberfläche der schiefen Eben zeigt. $F_P$ und $F_N$ hängen stark vom Winkel $\alpha$ ab.
3. Welche Konsequenz hat die Reibung für die Energieerhaltung? Wir kennen ja alle den Begriff „Reibungsverlust“. Es besagt, dass die Energie aus dem System verloren geht. Dann kann aber das System nicht mehr als abgeschlossen betrachtet werden. Wenn wir aber die Menge an Energie, die durch Reibung verloren geht kennen, können wir wieder mit dem Energieerhaltungssatz rechnen. Dabei ziehen wir diese „Reibungsverluste“ einfach aus der Gesamtenergie ab. Folgendes Beispiel soll dies anschaulich darstellen.
4. Beispiel: Rutschen auf einer schiefen Ebene mit Reibung
  Ein Objekt mit einer Masse von 100 [kg] rutscht auf einer schiefen Ebene (Neigungswinkel $\alpha = 30 \degree$) aus einer Höhe von $h=20 [m]$ hinunter. Mit welcher Geschwindigkeit $v$ kommt das Objekt unten an, wenn der Gleitreibungskoeffizient $\mu_G = 0,5$ beträgt?
  Gegeben und gesucht:
  Die Starthöhe $h=20[m]$, der Neigungswinkel der schiefen Ebene $\alpha = 30 \degree$, der Gleitreibungskoeffizient $\mu_G =0,5$ und die Masse des Objekts $m=100 [kg]$ sind angegeben. Gesucht ist die Aufprallgeschwindigkeit, d. h. die Geschwindigkeit unten am Fuß der schiefen Ebene ($h=0[m]$).
  
  Passende Formel:
  Oben ($h=20 [m]$) hat das Objekt nur die potenzielle Energie $E_{pot}= mgh$.
  Unten ($h=0 [m]$) hat das Objekt nur die kinetische Energie $E_{kin}= \frac 12 m v^2$.
  Entlang der zurückgelegte Strecke $s$ verliert das Objekt durch die Gleitreibung die Reibungsenergie $E_R= F_R \cdot s$. Anwendung der Herleitung der Gleitreibungskraft in Kapitel 3 liefert $E_R = \mu_G \cdot mg \cos (\alpha) \cdot s $
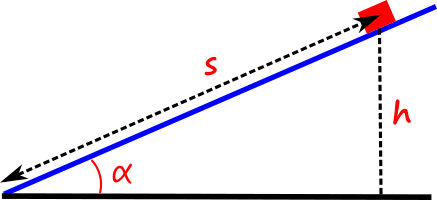
  Abbildung 2 zeigt, dass für die zurückgelegte Strecke $s$ auf der schiefen Ebene gilt: $s = h / \sin(\alpha)$. Einsetzen liefert $$\begin{aligned} E_R &= F_R \cdot s \\ &= \mu_G \cdot mg \cos (\alpha) \frac {h}{\sin(\alpha)} \end{aligned}$$ Aus Kapitel 2 wissen wir, dass $\frac {\cos(\alpha)}{\sin(\alpha)} = \cot (\alpha)$. Somit gilt $$E_R= \mu_G \cdot mg \cot (\alpha) \cdot h$$ Die Energieerhaltung besagt nun $E_{pot} – E_R = E_{kin}$, d. h. $$mgh – \mu_G \cdot mg \cot (\alpha) \cdot h= \frac 12 m v^2$$ Die Masse kann gekürzt werden, d.h. $$gh – \mu_G \cdot g \cot (\alpha) \cdot h= \frac 12 v^2$$ Auflösen nach v liefert $$v=\sqrt {2hg- 2 \mu_G \cdot g \cot (\alpha) \cdot h}$$ $$v=\sqrt {2hg (1- \mu_G \cdot \cot (\alpha))}$$ Beachte, dass in dieser Gleichung weder die Masse $m$ noch der Neigungswinkel $\alpha$ vorkommt. Diese Angaben benötigen wir nicht.
  
  Berechnung:
  Einsetzen der Werte liefert $$v = \sqrt {40 [m^2/s^2] (1-0,5 \cdot 0,57)} = 2,32 [m/s]$$

Schiefe Ebene — Abbildung 2: Für die zurückgelegte Strecke s auf der schiefen Ebene gilt $s = h / \sin(\alpha)$.

Zur Lernkontrolle