Vektorielle Betrachtung von Impuls
- Viele physikalische Größen sind Vektoren. Ein Vektor ist eine Größe, die eine Richtung und eine Länge hat (wie ein Pfeil mit einer Richtung und einer Länge).
- In Kapitel 2 haben wir gelernt, dass Kräfte Vektoren sind, da diese sowohl einen Betrag (Länge) als auch eine Richtung vorweisen.
- Nun betrachten wir den Impuls $$p= F \cdot t$$Die Kraft $F$ ist ein Vektor, d. h. $$\vec{F} = \begin{pmatrix} F_x \\ F_y \\ F_z \end{pmatrix}$$Die Zeit t hingegen ist eine Zahl (Mathematiker bezeichnen Zahlen als skalare Größen)
Wir bilden den Impuls, indem wir die Koordinaten des Kraftvektors mit der Zeit t multiplizieren, d.h. $$\vec{p} = \begin{pmatrix} F_x \cdot t \\ F_y \cdot t \\ F_z \cdot t \end{pmatrix}$$Wie man leicht erkennen kann, ist auch der Impuls ein Vektor! - Wenn eine vektorielle Größe mit einer Zahl multipliziert wird, dann erhalten wir wieder einen Vektor!
Vektorielle Betrachtung von Arbeit
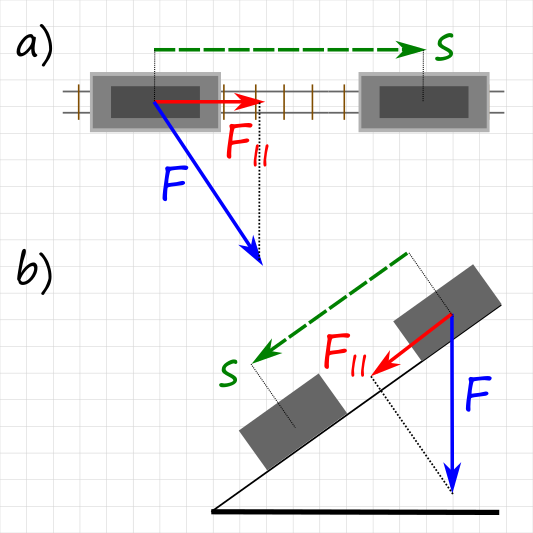
a) Ein Waggon auf Schienen wird mit Kraft F (blau) schräg zur Schienenrichtung gezogen. Die Bewegung erfolgt entlang der Schiene.
b) Die Bewegung eines Objekts auf einer schiefen Ebene erfolgt in Richtung der Schräge s und nicht in Richtung der einwirkenden Gewichtskraft F (blau).
In beiden Fällen muss die Kraft F in seine Bestandteile zerlegt werden, um die Kraft $F_{||}$ (rot) parallel zur Bewegungsrichtung zu bestimmen. Für die verrichtete Arbeit gilt in beiden Fällen $W = \vec F \cdot \vec s = F_{||} \cdot s$
- Wir haben gesehen, dass der Impuls eine vektorielle Größe ist, weil die Kraft ein Vektor ist.
- Die Arbeit hingegen ist eine skalare Größe d. h. eine Zahl und KEIN VEKTOR! Das Gleiche gilt auch für die Energie. Aber warum? Schließlich ist Arbeit $$W = F \cdot s$$ und F ist doch auch ein Vektor.
- Korrekt: F ist ein Vektor, aber s auch! Die Verschiebung s kann nach rechts, links, oben oder schräg erfolgen. Die Verschiebung s ist also ebenfalls ein Vektor, da sie eine Richtung besitzt.
- Wir haben es bei der Arbeit und der Energie also mit dem Produkt von zwei Vektoren zutun (s. Abbildung 1). Dafür haben wir in der letzten Lektion das Skalarprodukt kennen gelernt.
- Die Arbeit ist das Skalarprodukt der Kraft und der Strecke, d.h. $$W = \vec F \cdot \vec s$$Und wenn $\vec{F} = \begin{pmatrix} F_x \\ F_y \\ F_z \end{pmatrix}$ und $\vec{s} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$, dann gilt $$W = \begin{pmatrix} F_x \\ F_y \\ F_z \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} = F_x \cdot x +F_y \cdot y + F_z \cdot z$$
Vektorielle Betrachtung von Leistung
- Analog zur Arbeit ist auch die Leistung eine skalare Größe d. h. eine Zahl und kein Vektor!
- Darauf kann man auf zwei Wege kommen:
Weg 1: $P= \frac W t$ muss ein Skalar sein, da sowohl W als auch t skalare Größen sind.
Weg 2: $P= \vec F \cdot \vec v$ ist das Skalarprodukt der Kraft- und Geschwindigkeitsvektors und daher eine skalare Größe (d.h. eine Zahl und kein Vektor).