-
- In Kapitel 2 haben wir gelernt, dass viele physikalische Größen Vektoren sind. Ein Vektor ist eine Größe, die eine Richtung und eine Länge hat.
- Die Länge eines Vektors $\vec{v}$ wird auch als sein Betrag bezeichnet und mit $\lvert \vec{v} \rvert$ oder $\lVert \vec{v} \rVert$ dargestellt. Für den Vektor $\vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$ ist der Betrag (die Länge) $\lvert \vec{v} \rvert = \sqrt{x^2+y^2+z^2}$.
- Ein Vektor mit der Länge 1 wird als einen Einheitsvektor bezeichnet.
- Betrachten wir den Vektor $\vec{a} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$ und den Vektor $\vec{b} = \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix}$. Wir multiplizieren diese Vektoren, indem wir die x-Koordinaten miteinander, die y-Koordinaten miteinander, die z-Koordinaten miteinander multiplizieren und anschließend die Summe bilden, d.h. alles aufaddieren. Mathematisch schreiben wir das so $$\vec{a} \cdot \vec{b} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \cdot \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix}$$ $$\boxed{\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z}$$ Dieses Produkt zweier Vektoren, das eine einzige Zahl liefert, bezeichnen wir als das Skalarprodukt.
- Ein Beispiel: Das Skalarprodukt der Vektoren $\vec{a} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} 5 \\ 3 \\ -1 \end{pmatrix}$ beträgt $$\begin{aligned} \vec{a} \cdot \vec{b} &= 2 \cdot 5 -1 \cdot 3 + 4 \cdot (-1) \\ &= 10 -3 -4 \\ &=3 \end{aligned} $$
- Es gibt eine zweite Möglichkeit das Skalarprodukt zu bilden.
Betrachten wir zwei Vektoren $\vec a$ und $\vec b$ von denen wir die Länge (d. h. den Betrag) kennen. Diese Längen bezeichnen wir mit $\lvert \vec{a} \rvert$ und $\lvert \vec{b} \rvert$. Nun brauchen wir nur noch den Winkel zwischen diesen Vektoren. Diesen bezeichnen wir mit $\gamma$. Wenn wir die Länge zweier Vektoren und den Winkel, den sie einschließen kennen, können wir folgendermaßen ihr Skalarprodukt berechnen $$\boxed{\vec{a} \cdot \vec{b} = \lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert \cdot \cos {\gamma} }$$ Diese Definition des Skalarprodukts ist viel wichtiger und hilfreicher! - Ein Beispiel: Vektor $\vec{a}$ hat die Länge $\lvert \vec a \rvert = 5 $ und Vektor $\vec{b}$ die Länge $\lvert \vec b \rvert = 2 $. Der Winkel zwischen $\vec a$ und $\vec b$ beträgt $\gamma = 60 \degree$. Ihr Skalarprodukt lautet $$\begin{aligned} \vec{a} \cdot \vec{b} &= 5 \cdot 2 \cdot \cos {60 \degree} \\ &= 10 \cdot 0,5 \\ &= 5 \end{aligned}$$
Eigenschaften und Anwendungen
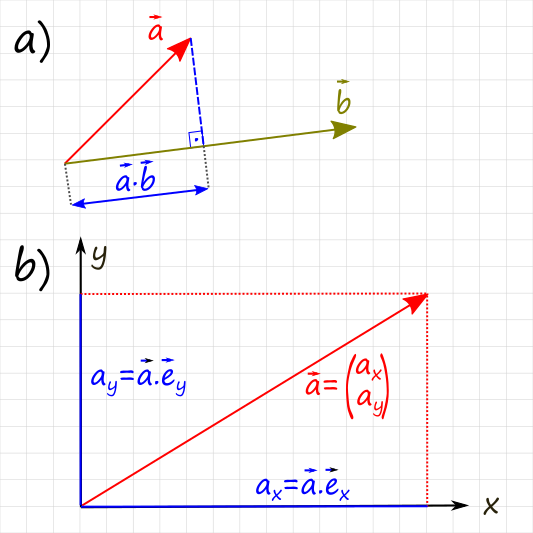
Abbildung 1b: Das Ablesen von Koordinaten eines Vektors ist durch Bildung
von Skalarprodukt mit den Einheitsvektoren der Koordinatenachsen möglich.
- Betrachten wir das Skalarprodukt zweier Vektoren $$\vec{a} \cdot \vec{b} = \lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert \cdot \cos {\gamma} $$ Wenn die Vektoren senkrecht aufeinander stehen ist natürlich $\gamma = 90 \degree$. Streber der Nation wissen, dass $cos (90 \degree) = 0$.
Das Skalarprodukt von zwei Vektoren, die senkrecht aufeinander stehen ist Null, d. h. $\vec{a} \cdot \vec{b} = 0$.
Mathematiker verwenden anstatt „senkrecht“ das Wort „orthogonal“ und anstatt „Null“ das Wort „Verschwinden“. Versuchen wir es nochmal als Mathematiker:
Das Skalarprodukt orthogonaler Vektoren verschwindet! (Yeah!). - Betrachten wir das Skalarprodukt zweier Vektoren $$\vec{a} \cdot \vec{b} = \lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert \cdot \cos {\gamma} $$ Wenn die Vektoren parallel zu einander stehen ist natürlich $\gamma = 0 \degree$. Streber der Nation wissen, dass $cos (0 \degree) = 1$.
Das Skalarprodukt von zwei parallelen Vektoren ist gleich dem Produkt ihrer Längen, d. h. $\vec{a} \cdot \vec{b} = \lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert $
Ein besondere Fall ist, wenn wir einen Vektor mit sich selbst multiplizieren. Ein Vektor ist immer zu sich selbst parallel, d. h. $\vec{a} \cdot \vec{a} = (\lvert \vec{a} \rvert)^2$ - Und nun zur besten Eigenschaft des Skalarprodukts: „Die orthogonale Projektion“ (auf Deutsch: der senkrechte Lot)
Betrachten wir die Abbildung 1a: Durch einen senkrechten Lot kann der Vektor $\vec a$ auf den Vektor $\vec b$ projiziert werden. Das Skalarprodukt $\vec a \cdot \vec b$ stellt dann die Projektionslänge von $\vec a$ auf $\vec b$ dar. - Jedes Mal, wenn wir die Koordinaten eines Vektors ablesen, bilden wir senkrechte Lote zu den Koordinatenachsen. Mathematisch bilden wir also Skalarprodukte (Abbildung 1b).
- Das zweidimensionale Koordinatensystem, dass wir in der Schule verwenden, ist zwischen der x-Achse mit dem Vektor $\vec{e_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$ und der y-Achse mit dem Vektor $\vec{e_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ aufgespannt.
Beispiel: Welche Koordinaten hat der Vektor $\vec a = \begin{pmatrix} 5 \\ -2 \end{pmatrix}$?
Natürlich 5 und -2. Aber wie kommen wir dazu?
Indem wir Skalarprodukte bilden:
x-Koordinate $$a_x= \vec a \cdot \vec {e_x} = \begin{pmatrix} 5 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} =5 +0 = 5$$ y-Koordinate $$a_x= \vec a \cdot \vec {e_y} = \begin{pmatrix} 5 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} =0 -2 = -2$$ Hinweis für die Streber der Nation: Ein Koordinatensystem, welches zwischen den Vektoren $\vec{e_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$ und $\vec{e_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ aufgespannt wird, bezeichnet man als ein Kartesisches Koordinatensystem.